|
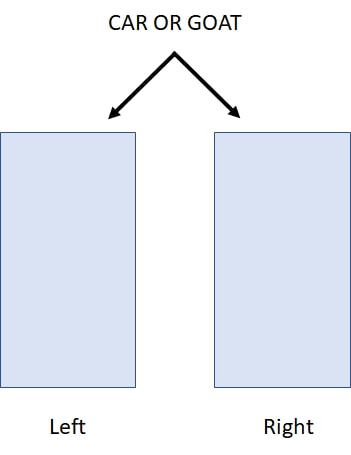
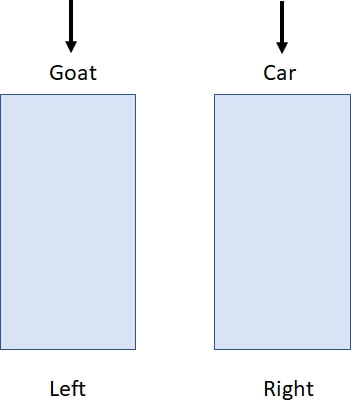
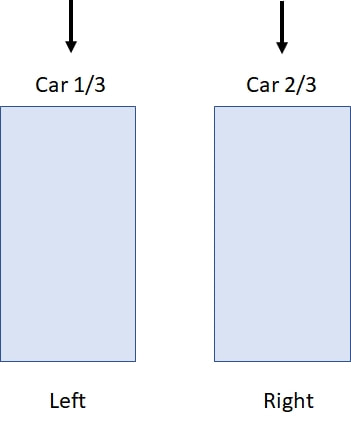
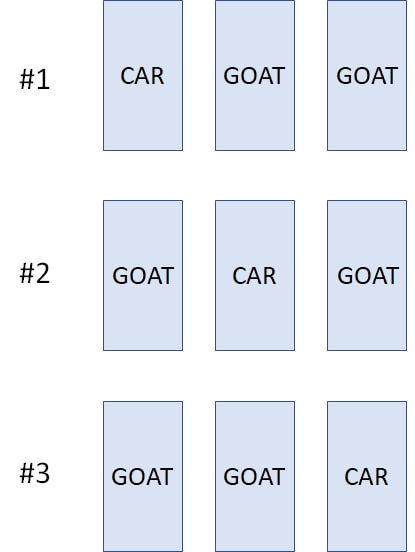
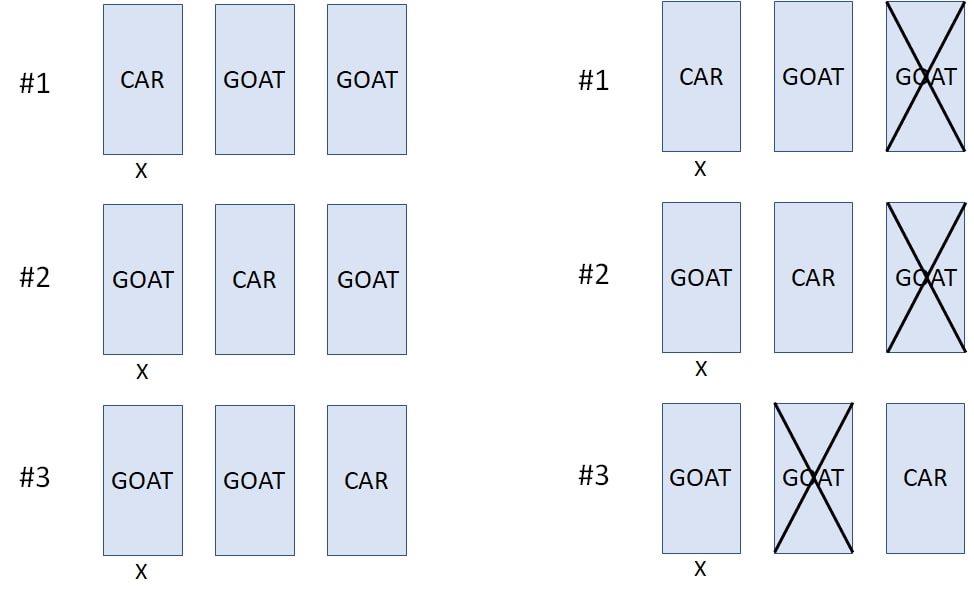
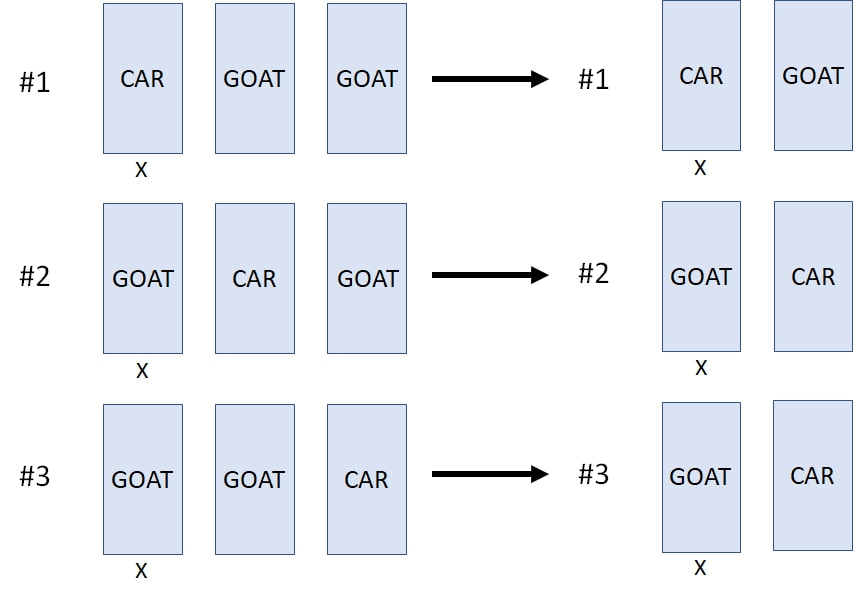
I have previously mentioned in my blog the so-called Monty Hall Puzzle (named after a Canadian-American game show host). The puzzle involves the setup of a recurring game show where you are given a choice between three doors. Behind one door is a car, and behind the other two doors there are goats. You pick one door, and the game show host proceeds to open one of the remaining two doors revealing a goat (note: he knows where the car and the goats are, and after a player makes a choice, he always opens a door revealing a goat). The game show host then asks you if you want to switch your original selection to the other door. The question is: is it to your advantage to switch your choice of doors? This puzzle was sent in 1990 to an American writer, Marylyn vos Savant, who writes a weekly column for the magazine Parade where she solves puzzles for her readers. Marylyn at the time was recognized by the folks at Guinness World Records to be the person with the highest IQ in the world before that category was eliminated from their world record groupings in 1990. Marylyn examined the puzzle and in a very matter of fact way replied that if you switch your original door choice, your chances of winning will be 2/3, but if you retain your original choice, your chances of winning will be 1/3. This ignited a huge controversy that degenerated into an insult fest. The effort to verify Marylyn’s answer ended up involving tens of thousands of people ranging from students at schools to mathematicians and statisticians from prestigious research centers in the United States. She was eventually proven to be right. Over the years I’ve brought up this puzzle several times, and the reactions that I’ve got from people when I mention the solution and try to explain it have amazed me. Their demeanor changes. Some get impatient, and some even get frankly hostile. The solution to this puzzle seems to be so counterintuitive that people feel that you are peddling nonsense to them when you reveal the correct answer, and they get mad at you. In their minds it’s as if they are holding a cup, and I come along trying to convince them that they are not holding a cup. But the solution is correct. Yes, at the end there are two doors. Yes, behind one is a goat, and behind the other is a car. But no, the probability of winning the car is not 50%. If you keep your original choice, it is 33.3% (1/3) and if you switch it is 66.6% (2/3). And in case this doesn’t amaze/confuse you enough, consider the following: Suppose that while you are in the game show pondering whether to change your original choice, a person comes in from the street. This person doesn’t know anything about what has been happening in the game show. Suppose that this person is asked to choose one of the two doors that you are looking at. What is the probability that this person would win the car if the person chooses one of these two doors at random? The amazing answer is 50%! In order to understand what’s going on, first we will start with two doors as shown in figure-1. In a random fashion, I place a car behind one of the doors and a goat behind the other, and I ask you to pick a door. Your chances of winning the car are 50%. If we repeat this trial 18 times, you will win the car 9 times out of 18 (statistically speaking). So far so good. But now suppose that I do not place the car behind the doors in a random fashion. Suppose that I always place the car behind the door on the right (figure-2). If we repeat the trial 18 times and you choose a door at random every time, you will still win the car 9 times out of 18 (50%). However, if somebody tips you off that I will always place the car behind the door on the right, and you adapt your door picking strategy to always select the door on the right (non-random choosing), you will win a car 18 times out of 18 (100%)! Of course, if you instead always pick the door on the left, you will never win a car. Please notice that in this example THERE ARE ONLY TWO DOORS, behind one is a car, and behind the other is a goat, YET if you pick the door on the left you will NEVER win a car. If you pick the door on the right, you WILL ALWAYS win a car. And if you pick at random between the two doors you will win the car HALF OF THE TIME! This illustrates the key point behind probability determination: randomness. If you know the allocation of the car to a given door is not random, you can use this information to increase your chance of winning (in the above case 100% by choosing the door on the right). Now suppose that we repeat the trial another 18 times, but I place the car behind the door on the left 6 times out of 18 (6/18 or 1/3: 33.3%), and I place the car behind the door on the right 12 times out of 18 (12/18 or 2/3: 66.6%) as shown in figure-3. If you choose a door at random, you will pick on the average the door on the left 9 times and win the car on 3 occasions, and the door on the right 9 times and win the car on 6 occasions for a grand total of 9 (6+3) times out of 18, or 50%. But again, if somebody tips you off to what I’m doing, and you always select the door on the right, you will win a car 12 times out of 18 (12/18 or 2/3: 66.6%). Of course, if you instead always pick the door on the left, you will win the car only 6 times out of 18 (6/18 or 1/3: 33.3%). Again, please notice: THERE ARE ONLY TWO DOORS, behind one a car, behind the other a goat, YET if you pick the one on the left you win a car 1/3 of the time. If you pick the one on the right, you win the car 2/3 of the time. And if you pick at random between the two doors, you win 50% of the time! At this point, even if you agree with me that lack of randomness can lead to different probabilities of winning the car when there are only two doors (depending on how you choose) you can still argue that increasing your chances of winning in the above examples depends on somebody tipping you off, in other words: cheating. But what if you could obtain this information without cheating? In the Monty Hall puzzle, there are three doors. Behind one there is a car, and behind the other two there are goats. So the three possible arrangements are #1 car-goat-goat, #2 goat-car-goat, and #3 goat-goat-car (see figure-4). IF the car is placed behind the doors at random, and you repeat the Monty Hall trial 18 times, the chance of picking the door with a car is 6 in 18 (1/3: 33.3%) whether you choose the doors at random or not. Then, after you make your choice, the game show host opens one of the two remaining doors revealing a goat and asks you if you want to change your initial pick. The key to understanding the answer to the Monty Hall puzzle is to realize that by opening the door and revealing a goat, the game show host has eliminated the element of randomness in the allocation of the car to the doors. By eliminating that extra door, the odds now favor the door opposite to the one you picked! Say that, for the sake of simplicity, out of the three doors (left, center, and right) you have chosen the door on the left (marked with an X under the door for the three possible arrangements: see below). That door will have a car behind it 1/3 of the time. But now the game show host opens one of the remaining doors revealing a goat (door crossed out). By doing this, the game show host changes the original possible three-door arrangement of #1 Car-Goat-Goat, #2 Goat-Car-Goat, and #3 Goat-Goat-Car, and converts it into a two-door arrangement: #1 Car-Goat, #2 Goat-Car, and #3 Goat-Car where your door of choice is the one on the left (marked with the X) as shown in figure-6. But notice that in the new two door scenario arrangements #2 and #3 are the same. The game show host has created a situation identical to the one depicted in the example of figure-3 where there are only two doors, and one of the doors is favored over the other when it comes to placing the car behind the doors (in this case the one opposite to the one you picked: the one on the right). Therefore, just like in the situation of figure-3, you can exploit this information by switching to the other door and increasing your probability of winning from 1/3 to 2/3. The difference, of course, is that in the example of figure-3 there was cheating involved (somebody tipped you off), whereas in the actual Monty Hall puzzle, your knowledge about how the setup came into being (the opening of the door revealing a goat) allows you to exploit it to improve your odds of winning the car. On the other hand, the person walking in from the street, who doesn’t have the information you have, will choose between the doors at random, so their chance of winning the car is 50%.
Many people automatically assume randomness when gauging the probability of an either-or event. At the end there are two doors, behind one is car and behind the other is goat, therefore thinking that there is a 50% chance of winning seems like a no-brainer. This may be why people are so confused and exasperated by the correct answer to the Monty Hall puzzle. But what my explanation illustrates is that if you can gain information about a setup and figure out that it is not random, you can use this information to increase your odds of winning by changing your picking strategy. The Monty Hall puzzle is, of course, just a puzzle, but it bears on how we conduct ourselves in the real world when making choices about either-or outcomes. Should I buy a mortgage on this house? Will the housing market go up or down? Should I buy the stock of this company? Will the stock go up or down? Should I begin looking for work? Will I get laid off or not? The probability of most real-life either-or events is determined by forces which are not random. If we understand probability and we identify these forces, we can make the odds work in our favor. Unfortunately, many people misjudge their chances or get dupped into believing false probability determinations, and they end up with, well…a goat. The Monty Hall Puzzle image by Cepheus is in the public domain, all other images belong to the author and can only be reproduced with permission.
0 Comments
 Monty Hall Puzzle Monty Hall Puzzle Marylyn vos Savant is an American writer who was recognized by the folks at Guinness World Records to be the person with the highest IQ in the world before that category was eliminated from their world record groupings in 1990. Marylyn writes a weekly column for the magazine Parade, where, among other things, she solves puzzles and answers questions that her readers send to her. In 1990, one reader sent her a puzzle (named the Monty Hall Puzzle after a Canadian-American game show host) that involved a game show where you are given a choice between 3 doors. Behind one door is a car, and behind the other 2 doors there are goats. You pick one door, and the game show host proceeds to open one of the remaining 2 doors revealing a goat. The game show host then asks you if you want to switch your original selection to the other remaining door. The question is: is it to your advantage to switch your choice of doors?  World Trade Center Towers World Trade Center Towers Marylyn replied in a very matter of fact way that the answer is “Yes, you should switch”. If you keep your original choice, the odds of winning the car are 1/3, but if you switch, the odds of winning the car are 2/3. This ignited a firestorm among her readers which included quite a number of scientists. She received thousands of letters telling her that there is no advantage in switching because, as there are 2 doors left, one with a goat and the other with a car, the probability of winning the car is 1/2. Of those that wrote letters to her, only 8% of the general public and 35% of scientists thought she was right. Marylyn wrote another column maintaining she indeed was right and tried to explain her reasoning, but to no avail. The insults started coming in. Many laypeople and scientists (including mathematicians and statisticians from prestigious research centers in the country) lectured her on probability and berated her intellect, some even suggesting that maybe women think about statistics differently. In response Marylin wrote a another column asking for a nationwide experiment to be carried out in math classes and labs, in essence reproducing the problem using 3 cups and a penny. After this she was vindicated. The experiment she suggested along with simulations performed using computers, proved that she was indeed correct, and many former skeptics wrote letters of contrition apologizing for insulting her. By the time she published her last column on the subject, 56% percent of the general public and 71% of scientists (the majority) accepted that she was right. The process outlined above, displayed an initial phase of skepticism, followed by a second phase of analysis and corroboration of the claim. However, the case of the puzzle is clear cut. There is no ambiguity. Everyone could perform the experiment and convince themselves of the truth (there are even online sites that allow you to do this now). And yet, despite this, there were still a significant percentage of individuals who did not accept Marylyn’s conclusion. The two phases mentioned above are also seen in the acceptance of counterintuitive scientific theories, although the complexity of the analyses is much greater and not accessible to everyone, and the opposition from the skeptics is much stronger. This is especially true in some dramatic situations involving science where the debate spreads into the social and political realms spanning conspiracy theories. One such case is the conspiracy theory that states that the collapse of the World Trade Center Towers after the attacks of 911 was produced by demolition charges and not as a direct result of the attacks. Among the buildings that collapsed, the case of Building 7 became a lightning rod for the conspiracy theorists because of the way it was damaged and the way it fell. Building 7 was one of the buildings in the World Trade center complex. It was not targeted by the terrorists, but rather when the World Trade Center Towers collapsed, this inactivated the pipes carrying water to the sprinkler system of Building 7, and burning debris from the towers ignited fires within the offices. The fires burned for several hours, and then Building 7 collapsed in a manner that reminded both laypeople and experts of a controlled demolition. Additionally, at this time the collapse of a steel frame building such as Building 7 was unheard of. This, along with a series of interpretations of actions and communications taking place that day, led a large number of people to express skepticism that Building 7 could have collapsed due to the fire. The above state of affairs represented the initial phase of what happens when people are confronted by something that counters their sense of how things should work. Skepticism in this phase is a reasonable reaction to the information being received. Among the several investigations conducted after 911, the National Institutes of Standards and Technology (NIST) conducted a thorough 3 year investigation that explained why building 7 collapsed in a manner reminiscent of a controlled demolition. In doing this they discovered a new type of progressive collapse which accounted for the collapse of the building which they dubbed fire-induced progressive collapse. Using simulations, they conclusively explained how a steel frame building such as Building 7 could be brought down by fires, and they ruled out other explanations. Some reasonable skeptics were still left unconvinced because, after all, no steel frame building had ever collapsed due to fire alone. However, this changed when the Plasco High-Rise building in Tehran (a steel frame building like Building 7) collapsed as a result of a fire in 2017. A very clear explanation of the above facts is presented by Edward Current in the video below.
Because of this and other investigations, the scientific community today accepts the explanation that Building 7 collapsed due to fire. This was the second phase where facts were gathered, research was carried out, and the issues were explained to the satisfaction of the majority. This is not to say that there aren’t some holdouts. For example the Architects and Engineers for 9/11 Truth is a group that has still refuses to accept these conclusions, and in their website they boast of having 3,141 plus architects and engineers that still espouse skepticism of the accepted explanation. However, considering there were 113,554 licensed architects in the US in 2017 and 1.6 million employed engineers in the US in 2015, you can see that these individuals represent just a minority of their professions that still cling to an irrational skepticism that is unwarranted. Such is the resistance some human beings display to accepting counterintuitive facts, whether they are the solutions to a fun puzzle or the explanations behind world changing events. The Monty Hall Problem image by Cepheus is in the public domain. |
Details
Categories
All
Archives
June 2024
|
 RSS Feed
RSS Feed